Perhatikan gambar di bawah ini!
Dapatkah kalian memilih panjang tangga yang bersandar di tembok menyerupai gambar di atas? Salah satu cara untuk memilih panjang tangga yakni dengan rumus Phytagoras. Lalu, apa itu rumus Phytagoras? Bagaimana penerapannya dalam kehidupan? Untuk menjawaban pertanyaan tersebut, pelajarilah bahan matematika ini dengan baik.
Rumus Phytagoras yakni rumus yang didapati dari Teorema Phytagoras. Teorema Phytagoras yakni teorema yang pertanda wacana keberhubungan sisi-sisi yang terdapat dalam sebuah segitiga siku-siku. Teorema ini pertama kali dikemukakan oleh seorang matematikiawan asal Yunani yang berjulukan Phytagoras.
Adapun suara Teorema Phytagoras yakni sebagai diberikut.
Dari teorema tersebut sanggup dibentuk sebuah rumus yang sanggup digambarkan sebagai diberikut.
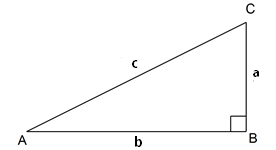
Misalkan dipunyai dengan siku-siku di B. Jika panjang sisi miring (hipotenusa) yakni c dan panjang sisi-sisi penyikunya (sisi selain sisi miring) yakni a dan b, maka teorema Phytagoras di atas sanggup dirumuskan sebagai diberikut.
c = sisi miring
a = tinggi
b = alas
Rumus Phytagoras umumnya dipakai untuk mencari panjang sisi miring segitiga siku-siku sebagai diberikut :
Kuadrat sisi AC = kuadrat sisi AB + kuadrat sisi BC. atau AC² = AB² + BC²
Rumus untuk mencari panjang sisi alas:
b² = c² - a²
Rumus untuk mencari sisi samping/tinggi segitiga:
a² = c² - b²
Rumus untuk mencari sisi miring segitiga siku-siku:
c² = a² + b²
Secara matematis, rumus Phytagoras biasa dipakai untuk memilih panjang sisi dari sebuah segitiga siku-siku. Untuk lebih jelasnya, perhatikan contoh-contoh soal di bawah ini.
1. Diketahui segitiga siku-siku ABC dengan siku-siku di B digambarkan sebagai diberikut.
Tentukan panjang sisi miring AC pada gambar di atas!
Jawab:
Karena segitiga di atas ialah segitiga siku-siku, maka berlaku rumus Phytagoras sebagai diberikut.
AC² = AB² + BC²
AC² = 8² + 6²
AC² = 64 + 36
AC² = 100
AC = √100
AC = 10
Jadi, panjang sisi AC pada segitiga siku-siku tersebut yakni 10 cm.
2. Sebuah segitiga siku-siku KLM dengan siku-siku di L digambarkan sebagai diberikut.
Tentukan panjang sisi KL pada gambar di atas!
Jawab:
Karena segitiga di atas ialah segitiga siku-siku, maka berlaku rumus Phytagoras sebagai diberikut.
KM² = KL² + LM²
KL² = KM² - LM²
KL² = 13² - 12²
KL² = 169 - 144
KL² = 25
KL = √25
KL = 5
Jadi, panjang sisi KL pada segitiga siku-siku tersebut yakni 5 cm.
3. Diketahui segitiga siku-siku DEF dengan siku-siku di E digambarkan sebagai diberikut.
Tentukan panjang sisi DE pada gambar di atas!
Jawab:
Karena segitiga DEF di atas yakni segitiga siku-siku, maka berlaku rumus Phytagoras sebagai diberikut.
DF² = DE² + EF²
DE² = DF² - EF²
DE² = 15² - 9²
DE² = 225 - 81
DE² = 144
DE = √144
DE = 12
Jadi, panjang sisi DE pada segitiga siku-siku tersebut yakni 12 cm.
4. Diketahui segitiga siku-siku ABC dengan siku-siku di B. Jika panjang sisi AB = 16 cm dan Panjang sisi BC = 12 cm. Tentukan panjang sisi AC pada gambar di atas!
Jawab:
Dari soal di atas sanggup digambarkan sebuah segitiga siku-siku sebagai diberikut.
Karena segitiga di atas ialah segitiga siku-siku, maka berlaku rumus Phytagoras sebagai diberikut.
c² = a² + b²
c² = 12² + 16²
c² = 144 + 256
c² = 400
c = √400
c = 20
Jadi, panjang sisi AC pada segitiga siku-siku ABC yang dimaksud di atas yakni 20 cm.
Selain untuk memilih panjang sisi segitiga siku-siku, rumus Phytagoras juga dipakai untuk memilih jenis dari sebuah segitiga. Apakah sebuah segitiga termasuk dalam jenis segitiga siku-siku, segitiga lancip, atau segitiga tumpul. Lalu, bagaimana cara kita memilih jenis segitiga dengan rumus Phytagoras itu?
Untuk memilih jenis segitiga dengan teorema Phytagoras, maka kita harus membandingkan kuadrat sisi terpanjang dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.
Misalkan dipunyai segitiga siku-siku dengan panjang sisi miringnya (sisi terpanjang) yakni c, dan panjang sisi-siki penyikunya yakni a dan b, maka:
Untuk lebih jelasnya, perhatikan contoh-contoh soal di bawah ini.
misal Soal:
Sebuah segitiga siku-siku ABC dengan siku-siku di B. Tentukan jenis segitiga tersebut apabila diketahui panjang sisi AB = 8 cm, BC = 15 cm, dan AC = 20 cm !
Jawab:
Misalkan a yakni sisi terpanjang dan b, c yakni dua sisi lainnya, maka diperoleh:
c = 20 cm, b = 8 cm, a = 15 cm.
c² = 20² = 400
a² + b² = 8² + 15² = 64 + 225 = 289
Karena
c² > a² + b²
400 > 289
maka segitiga ABC termasuk dalam segitiga tumpul.
misal Soal:
Tentukan jenis segitiga diberikut kalau diketahui panjang sisi-sisinya yakni 10 cm, 12 cm, dan 15 cm !
Jawab:
Misalkan c yakni sisi terpanjang dan b, a yakni dua sisi lainnya, maka diperoleh:
c = 15 cm, b = 10 cm, a = 12 cm.
c² = 15² = 225
a² + b² = 12² + 10² = 144 + 100 = 344
Karena
c² < a² + b²
225 < 344
maka segitiga tersebut termasuk dalam segitiga lancip.
Perhatikan beberapa bilangan di bawah ini.
3, 4, dan 5
6, 8, dan 10
5, 12, dan 13
Bilangan-bilangan yang ada di atas yakni bilangan-bilangan yang memenuhi hukum rumus Phytagoras. Bilangan-bilangan yang demikian itu dinamakan Tripel Phytagoras. Adapun bilangan Tripel Phytagoras sanggup didefinisikan sebagai diberikut.
Pada umumnya, Tripel Phytagoras terbagi menjadi dua yaitu Tripel Phytagoras Primitif dan Tripel Phytagoras Non-Primitif. Tripel Phytagoras Primitif yakni Tripel Phytagoras yang tiruana bilangannya mempunyai FPB sama dengan 1. misal dari bilangan Tripel Phytagoras Primitif yakni 3, 4, dan 5 serta 5, 12, 13.
Sedangkan Tripel Phytagoras Non-Primitif yakni Tripel Phytagoras yang bilangan-bilangannya mempunyai FPB tidak spesialuntuk sama dengan satu. contohnya yakni 6, 8, dan 10; 9, 12, dan 15; 12, 16, dan 20; serta 15, 20, dan 25.
Pola angka pythagoras (Triple pythagoras) berkhasiat untuk menuntaskan soal pythagoras dengan gampang, diberikut pola angka (triple pythagoras) tersebut:
a - b - c
3 – 4 – 5
5 – 12 – 13
6 – 8 – 10
7 – 24 – 25
8 – 15 – 17
9 – 12 – 15
10 – 24 – 26
12 – 16 – 20
12 – 35 – 37
13 – 84 – 85
14 – 48 – 50
15 – 20 – 25
15 – 36 – 39
16 – 30 – 34
17 – 144 – 145
19 – 180 – 181
20 – 21 – 29
20 – 99 – 101
Dan masih banyak lainnya.
Ket:
a = tinggi segitiga
b = ganjal segitiga
c = sisi miring
misal Soal Menentukan Jarak Kaki Tangga dengan Tembok
Perhatikan gambar di bawah ini dengan cermat.
Diketahui sebuah tangga disandarkan pada tembok. Jika panjang tangga yakni 5 m dan tinggi temboknya yakni 4 m, tentukan jarak antara kaki tangga dengan temboknya!
Jawab:
Misalkan jarak antara kaki tangga dan tembok adalah x, maka untuk memilih nilai x sanggup dipakai Rumus Phytagoras sebagai diberikut ini.
sisi miring atau c = 5m
tinggi atau b = 4m
ditanyakan ganjal atau x
x² = c² - b²
c² = 5² - 4²
c² = 25 - 16
c² = 9
c = √9
c = 3
Jadi, jarak antara kaki tangga dan tembok yakni 3 m.
misal Soal Menentukan Jarak Titik Awal Keberangkatan ke Titik Akhir:
Perhatikan gambar diberikut ini.
Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 15 km ke arah utara. Sesudah hingga di Pelabuhan B, kapal tersebut berlayar kembali sejauh 36 km ke arah timur. Hitunglah jarak antara pelabuhan A dengan titik akhir!
Jawab:
Dari soal di atas sanggup dibentuk gambar dengan isu menyerupai yang ada di bawah ini.
ditanyakan sisi miring atau c
diketahui
b = 36km
a = 15km
maka:
Jarak pelabuhan A ke titik akhir
c² = 15² + 36²
c² = 225 + 1296
c² = 1521
c = √1521
c = 39
Jadi, jarak pelabuhan A ke titik selesai yakni 39 km.
Dapatkah kalian memilih panjang tangga yang bersandar di tembok menyerupai gambar di atas? Salah satu cara untuk memilih panjang tangga yakni dengan rumus Phytagoras. Lalu, apa itu rumus Phytagoras? Bagaimana penerapannya dalam kehidupan? Untuk menjawaban pertanyaan tersebut, pelajarilah bahan matematika ini dengan baik.
Pengertian Rumus Phytagoras
Rumus Phytagoras yakni rumus yang didapati dari Teorema Phytagoras. Teorema Phytagoras yakni teorema yang pertanda wacana keberhubungan sisi-sisi yang terdapat dalam sebuah segitiga siku-siku. Teorema ini pertama kali dikemukakan oleh seorang matematikiawan asal Yunani yang berjulukan Phytagoras.
Adapun suara Teorema Phytagoras yakni sebagai diberikut.
Pada sebuah segitiga siku-siku, kuadrat dari sisi terpanjang yakni sama dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.
Dari teorema tersebut sanggup dibentuk sebuah rumus yang sanggup digambarkan sebagai diberikut.
Rumus Phytagoras
c² = a² + b²Keterangan:
c = sisi miring
a = tinggi
b = alas
Rumus Phytagoras umumnya dipakai untuk mencari panjang sisi miring segitiga siku-siku sebagai diberikut :
Rumus untuk mencari panjang sisi alas:
b² = c² - a²
Rumus untuk mencari sisi samping/tinggi segitiga:
a² = c² - b²
Rumus untuk mencari sisi miring segitiga siku-siku:
c² = a² + b²
Menentukan Panjang Sisi Segitiga Siku-Siku
Secara matematis, rumus Phytagoras biasa dipakai untuk memilih panjang sisi dari sebuah segitiga siku-siku. Untuk lebih jelasnya, perhatikan contoh-contoh soal di bawah ini.
misal Soal Pythagoras (Pitagoras) dan Penyelesaiannya:
1. Diketahui segitiga siku-siku ABC dengan siku-siku di B digambarkan sebagai diberikut.
Jawab:
Karena segitiga di atas ialah segitiga siku-siku, maka berlaku rumus Phytagoras sebagai diberikut.
AC² = AB² + BC²
AC² = 8² + 6²
AC² = 64 + 36
AC² = 100
AC = √100
AC = 10
Jadi, panjang sisi AC pada segitiga siku-siku tersebut yakni 10 cm.
2. Sebuah segitiga siku-siku KLM dengan siku-siku di L digambarkan sebagai diberikut.
Tentukan panjang sisi KL pada gambar di atas!
Jawab:
Karena segitiga di atas ialah segitiga siku-siku, maka berlaku rumus Phytagoras sebagai diberikut.
KM² = KL² + LM²
KL² = KM² - LM²
KL² = 13² - 12²
KL² = 169 - 144
KL² = 25
KL = √25
KL = 5
Jadi, panjang sisi KL pada segitiga siku-siku tersebut yakni 5 cm.
3. Diketahui segitiga siku-siku DEF dengan siku-siku di E digambarkan sebagai diberikut.
Tentukan panjang sisi DE pada gambar di atas!
Jawab:
Karena segitiga DEF di atas yakni segitiga siku-siku, maka berlaku rumus Phytagoras sebagai diberikut.
DF² = DE² + EF²
DE² = DF² - EF²
DE² = 15² - 9²
DE² = 225 - 81
DE² = 144
DE = √144
DE = 12
Jadi, panjang sisi DE pada segitiga siku-siku tersebut yakni 12 cm.
4. Diketahui segitiga siku-siku ABC dengan siku-siku di B. Jika panjang sisi AB = 16 cm dan Panjang sisi BC = 12 cm. Tentukan panjang sisi AC pada gambar di atas!
Jawab:
Dari soal di atas sanggup digambarkan sebuah segitiga siku-siku sebagai diberikut.
Karena segitiga di atas ialah segitiga siku-siku, maka berlaku rumus Phytagoras sebagai diberikut.
c² = a² + b²
c² = 12² + 16²
c² = 144 + 256
c² = 400
c = √400
c = 20
Jadi, panjang sisi AC pada segitiga siku-siku ABC yang dimaksud di atas yakni 20 cm.
Menentukan Jenis Segitiga kalau Diketahui Panjang Sisinya
Selain untuk memilih panjang sisi segitiga siku-siku, rumus Phytagoras juga dipakai untuk memilih jenis dari sebuah segitiga. Apakah sebuah segitiga termasuk dalam jenis segitiga siku-siku, segitiga lancip, atau segitiga tumpul. Lalu, bagaimana cara kita memilih jenis segitiga dengan rumus Phytagoras itu?
Untuk memilih jenis segitiga dengan teorema Phytagoras, maka kita harus membandingkan kuadrat sisi terpanjang dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.
Misalkan dipunyai segitiga siku-siku dengan panjang sisi miringnya (sisi terpanjang) yakni c, dan panjang sisi-siki penyikunya yakni a dan b, maka:
- Jika c² < a² + b², maka termasuk segitiga lancip;
- Jika c² = a² + b², maka termasuk segitiga siku-siku;
- Jika c² > a² + b², maka termasuk segitiga tumpul.
Untuk lebih jelasnya, perhatikan contoh-contoh soal di bawah ini.
misal Soal:
Sebuah segitiga siku-siku ABC dengan siku-siku di B. Tentukan jenis segitiga tersebut apabila diketahui panjang sisi AB = 8 cm, BC = 15 cm, dan AC = 20 cm !
Jawab:
Misalkan a yakni sisi terpanjang dan b, c yakni dua sisi lainnya, maka diperoleh:
c = 20 cm, b = 8 cm, a = 15 cm.
c² = 20² = 400
a² + b² = 8² + 15² = 64 + 225 = 289
Karena
c² > a² + b²
400 > 289
maka segitiga ABC termasuk dalam segitiga tumpul.
misal Soal:
Tentukan jenis segitiga diberikut kalau diketahui panjang sisi-sisinya yakni 10 cm, 12 cm, dan 15 cm !
Jawab:
Misalkan c yakni sisi terpanjang dan b, a yakni dua sisi lainnya, maka diperoleh:
c = 15 cm, b = 10 cm, a = 12 cm.
c² = 15² = 225
a² + b² = 12² + 10² = 144 + 100 = 344
Karena
c² < a² + b²
225 < 344
maka segitiga tersebut termasuk dalam segitiga lancip.
Tripel Phytagoras
Perhatikan beberapa bilangan di bawah ini.
3, 4, dan 5
6, 8, dan 10
5, 12, dan 13
Bilangan-bilangan yang ada di atas yakni bilangan-bilangan yang memenuhi hukum rumus Phytagoras. Bilangan-bilangan yang demikian itu dinamakan Tripel Phytagoras. Adapun bilangan Tripel Phytagoras sanggup didefinisikan sebagai diberikut.
Tripel Phytagoras yakni bilangan-bilangan lingkaran nyata yang kuadrat bilangan terbesarnya mempunyai nilai yang sama dengan jumlah dari kuadrat bilangan-bilangan lainnya.
Pada umumnya, Tripel Phytagoras terbagi menjadi dua yaitu Tripel Phytagoras Primitif dan Tripel Phytagoras Non-Primitif. Tripel Phytagoras Primitif yakni Tripel Phytagoras yang tiruana bilangannya mempunyai FPB sama dengan 1. misal dari bilangan Tripel Phytagoras Primitif yakni 3, 4, dan 5 serta 5, 12, 13.
Sedangkan Tripel Phytagoras Non-Primitif yakni Tripel Phytagoras yang bilangan-bilangannya mempunyai FPB tidak spesialuntuk sama dengan satu. contohnya yakni 6, 8, dan 10; 9, 12, dan 15; 12, 16, dan 20; serta 15, 20, dan 25.
Pola angka pythagoras (Triple pythagoras) berkhasiat untuk menuntaskan soal pythagoras dengan gampang, diberikut pola angka (triple pythagoras) tersebut:
a - b - c
3 – 4 – 5
5 – 12 – 13
6 – 8 – 10
7 – 24 – 25
8 – 15 – 17
9 – 12 – 15
10 – 24 – 26
12 – 16 – 20
12 – 35 – 37
13 – 84 – 85
14 – 48 – 50
15 – 20 – 25
15 – 36 – 39
16 – 30 – 34
17 – 144 – 145
19 – 180 – 181
20 – 21 – 29
20 – 99 – 101
Dan masih banyak lainnya.
Ket:
a = tinggi segitiga
b = ganjal segitiga
c = sisi miring
Aplikasi Rumus Phytagoras dalam Permasalahan Sehari-Hari
Rumus Phytagoras banyak dijumpai dalam banyak sekali permasalahan sehari-hari. Berikut ini akan dijabarkan beberapa aplikasi rumus Phytagoras tersebut.misal Soal Menentukan Jarak Kaki Tangga dengan Tembok
Perhatikan gambar di bawah ini dengan cermat.
Diketahui sebuah tangga disandarkan pada tembok. Jika panjang tangga yakni 5 m dan tinggi temboknya yakni 4 m, tentukan jarak antara kaki tangga dengan temboknya!
Jawab:
Misalkan jarak antara kaki tangga dan tembok adalah x, maka untuk memilih nilai x sanggup dipakai Rumus Phytagoras sebagai diberikut ini.
sisi miring atau c = 5m
tinggi atau b = 4m
ditanyakan ganjal atau x
x² = c² - b²
c² = 5² - 4²
c² = 25 - 16
c² = 9
c = √9
c = 3
Jadi, jarak antara kaki tangga dan tembok yakni 3 m.
misal Soal Menentukan Jarak Titik Awal Keberangkatan ke Titik Akhir:
Perhatikan gambar diberikut ini.
Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 15 km ke arah utara. Sesudah hingga di Pelabuhan B, kapal tersebut berlayar kembali sejauh 36 km ke arah timur. Hitunglah jarak antara pelabuhan A dengan titik akhir!
Jawab:
Dari soal di atas sanggup dibentuk gambar dengan isu menyerupai yang ada di bawah ini.
ditanyakan sisi miring atau c
diketahui
b = 36km
a = 15km
maka:
Jarak pelabuhan A ke titik akhir
c² = 15² + 36²
c² = 225 + 1296
c² = 1521
c = √1521
c = 39
Jadi, jarak pelabuhan A ke titik selesai yakni 39 km.
Demikianlah bahan Rumus Pythagoras (Pitagoras) Beserta misal Soal dan Pembahasannya. Semoga Bermanfaat.[resky]
